[2편] 인공지능 발전에 큰 획을 그은 전설의 3대 논문 - The Perceptron / Backpropagation

이 글은 "한 권으로 끝내는 실전 LLM 파인튜닝" 도서를 읽고 정리한 글입니다.

 

Intro

1편 - Turing Machine에 이은 후속 글입니다.

https://ricky-dev.tistory.com/13

[1편] 인공지능 발전에 큰 획을 그은 전설의 3대 논문 - Computing Machinery and Intelligence

 

이번엔 나머지 2개의 논문을 한번에 정리해보려 합니다.

 

인공지능을 "어떻게" 학습시킬 것인가에 대해 나온 수많은 방법들 중 가장 영향을 끼친 개념인 'Perceptron'에 대해 소개하고, 이 이론 뒤로 왜 겨울이 찾아왔는지, 그리고 겨울을 극복해낸 "Backpropagation"은 어떤 개념인지를 보며 패러다임을 정리해봅시다.

 

우선, 퍼셉트론이라는 개념이 등장하기 전까지 연구되었던 연구들을 살펴봅시다.

퍼셉트론 개념이 나오기 전까지의 중요한 연구들

1. Warren McCulloch, Walter Pitts - 신경망 모델

여러 입력 신호의 합이 정해진 기준값(임계값, threshold)을 넘으면 뉴런이 활성화되고, 그렇지 않으면 비활성화되는 모델입니다.

인간의 신경망을 본떠 정보이론과 함께

퍼셉트론: 여러 입력 신호의 합들이 임계치를 넘으면 활성화되는 개념

개념화했다는 점에서 획기적이였으며, 이를 본떠서 만든 인공 신경망 모델이 퍼셉트론입니다.

2. Donald Hebb - Hebbian Learning

또한, Hebb는 신경 가소성 원리를 제시하는데, 이는 뇌의 뉴런들이 동시에 활성화될 때, 그들 사이의 연결이 강해진다는 원리입니다.

뉴런들의 시너지에 대해 집중하며, 뉴런들이 상호작용하면서 스스로 학습한다는 점을 시사하는 점에서 의의를 가집니다.

 

Perceptron

이전 연구들을 기반으로, Rosenblatt와 연구진들은 "The Perceptron: A Probablistic Model for Information Storage and Organization in the Brain" 이라는 논문을 발표했습니다. 이 논문에서 퍼셉트론을 처음 소개하게 됩니다.

 

퍼셉트론은, 인간의 뇌세포인 뉴런을 모방하여 만든 간단한 인공 신경망 모델입니다.

저는 특히, 책에서 퍼셉트론을 연결주의 접근법이라는 관점에서 설명해준 것이 인상적이였습니다.

퍼셉트론은 연결주의 접근법을 따릅니다. 이 접근법에 따르면, 정보는 고정된 형태로 저장되어 필요할 때마다 동일한 방식으로 인출되는 코드화된 기억 방식이 아니라, 활성화된 뉴런들 사이의 새로운 연결 또는 경로를 통해 저장되며, 이는 뉴런 간의 연결 강도로 표현됩니다.
연결주의 접근법의 특징은 특정 자극과 반응 사이의 확률적 관계를 학습한다는 것입니다. 또한, 신경망의 연결이 정적이지 않고 경험에 따라 변한다는 점도 중요한 특징입니다.

 

선형적 분리

퍼셉트론 시스템은 ‘통계적 패턴’을 인식하기에, 두 가지의 서로 다른 유형의 입력을 무작위로 줘도, 이를 스스로 구분해낸다. 이처럼 퍼셉트론이 두 종류의 입력을 구분할 수 있는 능력을 ‘선형적 분리’라고 한다.

• 다시 말해, 두 자극을 구분할 수 있는 선을 하나 찌이익 그을 능력이 있다! 이 말이다.

로젝블랫이 말한 퍼셉트론의 한계

1. 인공지능의 발전을 위해선 완전히 새로운 접근 방식이 필요하다. 기존 원칙의 단순한 개선으로는 충분치 않으며, 근본적으로 다른 원칙이 필요하다.
   ⇒ 아직까지도 해결해야 할 문제로 남아있습니다. GPT, BERT 등의 트랜스포머 기반 모델들 역시, 아직 “근본적으로 다른 원칙”은 아니다.
2. 퍼셉트론 모델은 시간적 요소를 고려하지 않았다. 인간의 인지 과정에서 시간적 패턴 인식이 중요한 역할을 하는데, 이를 고려하지 않은 퍼셉트론은 한계가 있을 수 밖에 없다.
   ⇒ RNN, LSTM의 등장이 시간적 패턴 인식에서 많은 진전을 보였지만, 인간의 복잡한 시간 인식과 처리 능력을 완전히 모방한 건 아니기에 오늘날에도 여전히 한계점으로 남아있습니다.
3. 퍼셉트론이 상대적 판단과 관계의 추상화에서 한계를 보인다. 단순 패턴 인식,분류는 할 수 있어도, 두 자극 간의 관계를 인식하는 데 어려워한다.
   ⇒ 최근에는 ResNet, YOLO 등이 이미지 속 객체를 빠르고 정확하게 인지하고, GPT-4, Claude 등의 LLM의 등장은 멀티모달 추론 능력을 보여준다.
4. 퍼셉트론이 선형적으로만 분리 가능한 문제들만 해결할 수 있다.
   ⇒ 인공지능의 1차 겨울을 도래시킨 원인인데, 뒤에서 나오는 MLP와 Back-Propagation이 이를 해결한다.
5. 퍼셉트론 이론은 아직 초기 단계다. 인간의 복잡한 학습 메커니즘을 완전히 설명하거나 모방하기에는 아직 부족하다.

여기서 가장 중대한 영향을 끼친 한계는 4번이라고 생각합니다.

'퍼셉트론' 개념이 소개된 이유, 수많은 연구원들이 인공지능 업계에 뛰어들며 많은 발전을 해왔지만, 선형적 분리라는 제한 내에서 할 수 있는 영역은 한계가 있었기에, 이를 타파할 기법이 보이지 않는 한 발전할 수 없었기 때문이죠.

조금 더 자세히 살펴볼까요?

 

퍼셉트론의 한계 4 - 선형적으로만 분리 가능한 문제들만 해결한다.

두 개의 자극을 분류해낼 수 있다! 가 퍼셉트론이 뜬 이유인데, 분류해내지 못하는 유형이 있었습니다.

AND, NAND, OR gate는 줄 하나로 하얀색과 검은색을 구분할 수 있지만…XOR는 두 개가 필요하다는 점입니다.

XOR gate는 선 하나로 표현할 수가 없다는 사실..

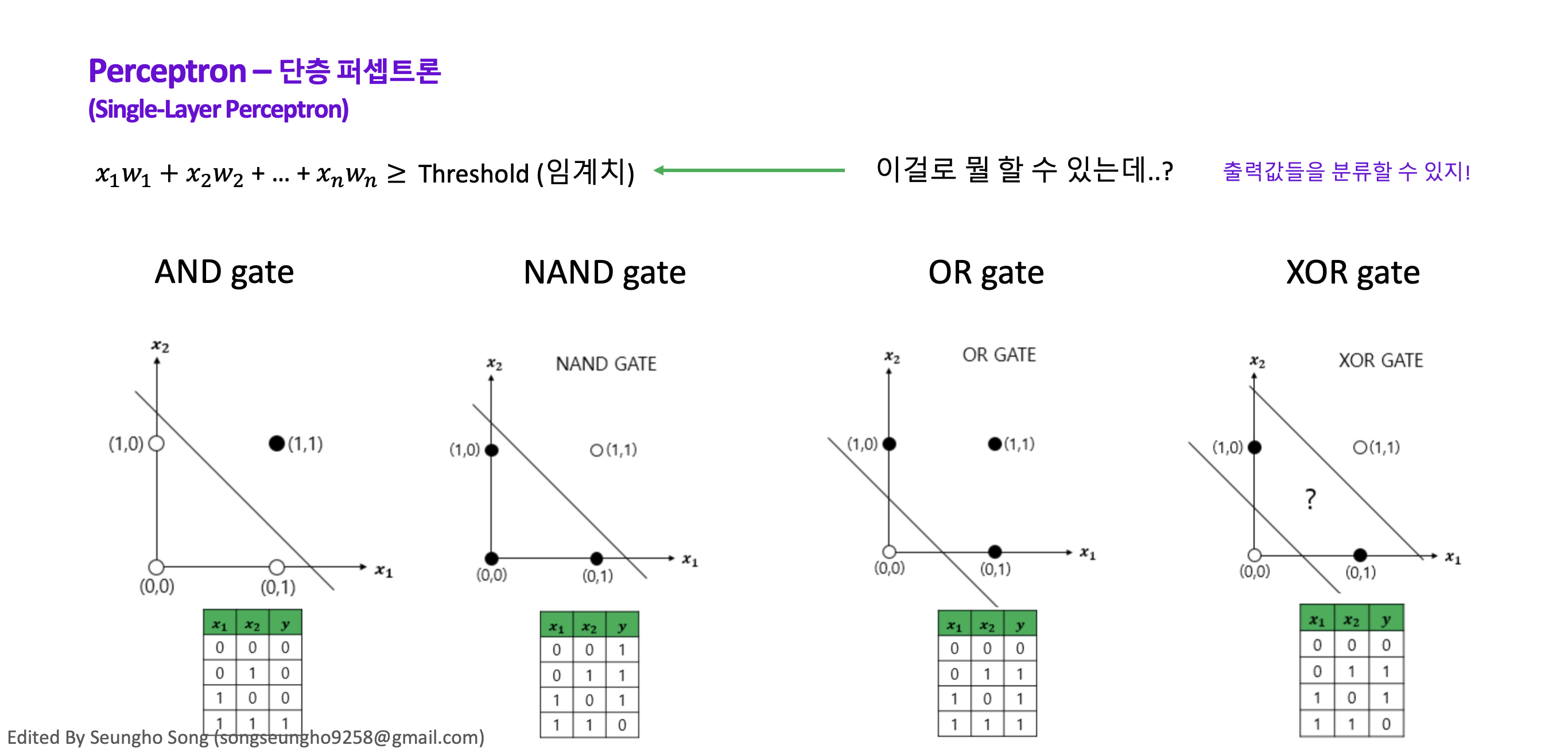
이를 보고, 퍼셉트론은 비선형적인 문제에는 적용할 수 없다는 사실을 깨달았죠.

사람들은 이걸 보고, 이게 맞나..? 라는 생각을 합니다. 사람의 지능은 분명 여러 가지 자극들을 처리하며 판단하는데, 고작 2가지 자극에서도 이런 한계가 있는게 인공지능이라는 점에서 실망을 하고, 이는 곧 인공지능의 1차 겨울이 도래하는 계기가 됩니다.

 

근데 선형과 비선형은 무슨 차이일까?

처음으로 선형과 비선형에 대해 생각나는 건 아마, “직선”과 “곡선”이다.

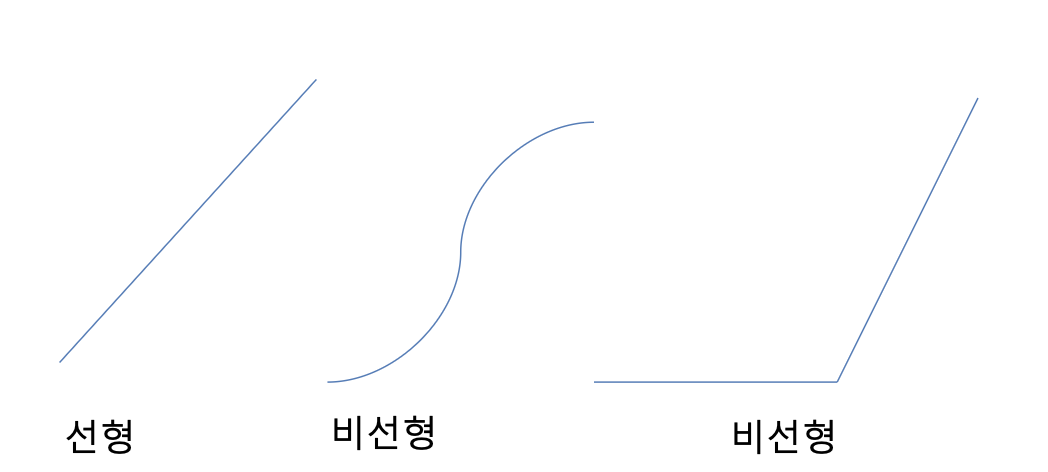
틀린 말은 아니지만, 단순히 이렇게만 구분하기에는 잘 안 와 닿습니다. 조금 더 이해하기 쉽게 보면 아래와 같습니다.

• 선형 함수 (Linear Function) : 출력이 입력의 상수배만큼 변하는 함수.
  • 즉, 직선 1개로 그릴 수 있는 함수!
• 비선형 함수 (Nonlinear Function) : 입출력 관계가 단순한 비례 관계를 벗어나는 함수.
  • 직선 1개로 그릴 수 없는 함수!
  • 작은 입력 변화가 큰 출력 변화를 일으키거나, 그 반대의 경우도 있을 수 있습니다.

이 때, 선형 함수는 여러가지 한계를 갖게 됩니다.

1. 아무리 많이 쌓아도 단순 선형 변환으로 축소됩니다.

이게 무슨 의미냐면, 다층 퍼셉트론(MLP) 구조라 한들 선형 함수를 아무리 많이 쌓아봤자, 결국엔 선형 함수가 된다는 의미입니다.

 

2. 미분 2번만에 0이 됩니다.

가중치를 업데이트하기 위해 역전파 과정을 취하려면 Gradient를 구해야 하는데, 이를 위해 선형 함수를 연속적으로 미분해야 하지만, 금방 미분값이 0이 되어버리는 불상사가 발생하죠..

즉, 업데이트가 안됩니다!

 

Backpropagation

그래서, 힌튼 교수님은 더더욱 비선형 함수에 집중하게 됩니다. 사실 안 쓸 이유가 없게 되죠.

• 입출력이 비례하지 않으니까, 다양한 변화량을 관측할 수 있게 됩니다.
• 역방향 학습에서 미분을 해도 0이 되지 않습니다.

이러한 특징 덕분에, 비선형 함수와 함께 진짜 역전파 업데이트를 써먹을 수 있게 되었습니다.

그래서 Learning representations by back-propagating errors 라는 논문을 발표하게 되죠.

순전파와 역전파의 반복을 통해 모델이 학습되는 과정은 아래와 같습니다.

1. 신경망은 입력을 받아 예측한다. (순전파)
2. 예측값과 실제 정답 사이의 오차 (loss)를 계산한다.
3. 오차를 출력층에서 시작해 입력층 방향으로 거꾸로 전파하면서, 각 층의 가중치를 업데이트한다. (역전파)
4. 업데이트된 가중치로 다시 신경망은 입력을 받아 예측한다. (Update 된 순전파)

여기서도 볼 수 있듯이, 기울기를 통해 업데이트값을 정할 수 있기에, 더더욱 미분에 대한 중요도가 높아지죠.

역전파 개념을 통해 현대 머신러닝의 발전이 획기적으로 일어날 수 있게 되었습니다.

 

 

이번에는 패러다임의 흐름을 따라가는 정도로만 알아보는 게 목적이기에, 역전파에 대한 자세한 개념은 다음 포스트에서 다뤄보도록 하겠습니다.